BÀI TẬP CỰC TRỊ CỦA HÀM SỐ PHẦN 2
CỰC TRỊ CỦA HÀM SỐ PHẦN 2. Ngoài phần lý thuyết, nhà trường sẽ kèm theo những bài tập để củng cố kiến thức cho các em tự tin bước vào kỳ thi THPT Quốc Gia.
I. TÓM TẮT KIẾN THỨC VỀ CỰC TRỊ CỦA HÀM SỐ PHẦN 2.
1. Định nghĩa
Cho hàm số y = f(x) liên tục trên khoảng (a ; b) và điểm x0 ∈ (a ; b).
– Nếu tồn tại số h > 0 sao cho f(x) < f(x0), ∀x ∈ (x0 – h ; x0 + h), x ≠ x0 thì ta nói hàm số f đạt cực đại tại x0 .
– Nếu tồn tại số h > 0 sao cho f(x) > f(x0), ∀x ∈ (x0 – h ; x0 + h), x ≠ x0 thì ta nói hàm số f đạt cực tiểu tại x0 .
2. Định lí 1.
Cho hàm số y = f(x) liên tục trên khoảng K = (x0 – h ; x0 + h) (h > 0) và có đạo hàm trên K hoặc trên K ∖{ x0 }.
Nếu {f′(x)>0|∀(x0−h;x0)f′(x)<0|∀(x0;x0+h) thì x0 là điểm cực đại của hàm số
Nếu {f′(x)<0|∀(x0−h;x0)f′(x)>0|∀(x0;x0+h) thì x0 là điểm cực tiểu của hàm số
3. Định lí 2.
Cho hàm số y = f(x) có đạo hàm cấp hai trên khoảng K = (x0 – h ; x0 + h) (h > 0).
– Nếu f ‘(x0) = 0, f ”(x0) > 0 thì x0 là điểm cực tiểu của hàm số f.
– Nếu f ‘(x0) = 0, f ”(x0) < 0 thì x0 là điểm cực đại của hàm số f.
4. Quy tắc tìm cực trị
a. Quy tắc 1
– Tìm tập xác định.
– Tính f ‘(x). Tìm các điểm tại đó f ‘(x) bằng 0 hoặc f ‘(x) không xác định.
– Lập bảng biến thiên.
– Từ bảng biến thiên suy ra các điểm cực trị.
b. Quy tắc 2
– Tìm tập xác định.
– Tính f ‘(x). Tìm các nghiệm xi của phương trình f ‘(x)=0.
– Tính f ”(x) và f ”(xi) suy ra tính chất cực trị của các điểm xi.
(Chú ý: nếu f ”(xi)=0 thì ta phải dùng quy tắc 1 để xét cực trị tại xi).
II. BÀI TẬP. DẠNG 1: TÌM CỰC TRỊ CỦA HÀM KHI BIẾT Y, Y’
- PHẦN TRẮC NGHIỆM:

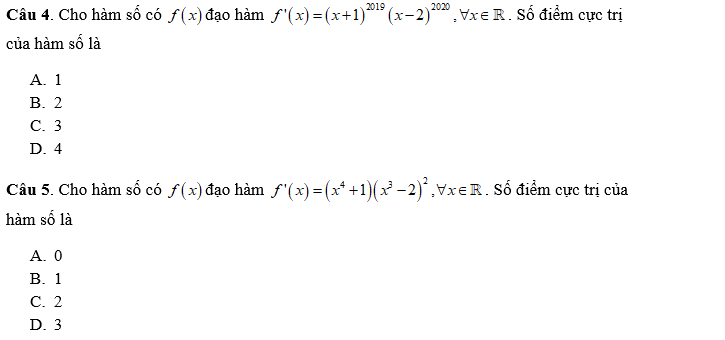
- PHẦN TỰ LUẬN:
- Tìm cực trị của các hàm số sau:

“NGỌC VIỄN ĐÔNG - MỖI HỌC SINH MỘT VIÊN NGỌC”