BÀI TẬP HÀM SỐ LŨY THỪA, MŨ, LOGARIT
HÀM SỐ LŨY THỪA, MŨ, LOGARIT. Ngoài phần lý thuyết, nhà trường sẽ kèm theo những bài tập để củng cố kiến thức cho các em tự tin bước vào kỳ thi THPT Quốc Gia.
- Xem video bài giảng lý thuyết tại HÀM SỐ LŨY THỪA, MŨ, LOGARIT
A. MỘT SỐ KIẾN THỨC CẦN NHỚ VỀ HÀM SỐ LŨY THỪA, MŨ, LOGARIT
I. Hàm số mũ
1. Định nghĩa
- Hàm số mũ là hàm số có dạng y= ax, hàm số lôgarit là hàm số có dạng y = logax ( với cơ số a dương khác 1).
2. Tính chất của hàm số mũ y= ax ( a > 0, a# 1).
- Tập xác định: .
- Đạo hàm: ∀x ∈ ,y’= axlna.
- Chiều biến thiên
+) Nếu a > 1 thì hàm số luôn đồng biến
+) Nếu 0 < a < 1 thì hàm số lôn nghịch biến.
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành ( y= ax > 0, ∀x), và luôn cắt trục tung taih điểm ( 0;1) và đi qua điểm (1;a).
II. Hàm số loagarit
- Tập xác định: (0; +∞).
- Đạo hàm ∀x ∈ (0; +∞),y’ = 1xlna.
- Chiều biến thiên:
+) Nếu a> 1 thì hàm số luôn đồng biến
+) Nếu 0< a < 1 thì hàm số luôn nghịch biến
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
III. Chú ý
-
Vì e > 1 nên nếu a > 1 thì lna > 0, suy ra (ax)’ > 0,∀x và (logax)’ > 0, ∀x > 0;
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu 0 < a< 1thì lna < 0, (ax)’ < 0 và (logax)’ < 0, ∀x > 0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
B. BÀI TẬP VẬN DỤNG
- TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ
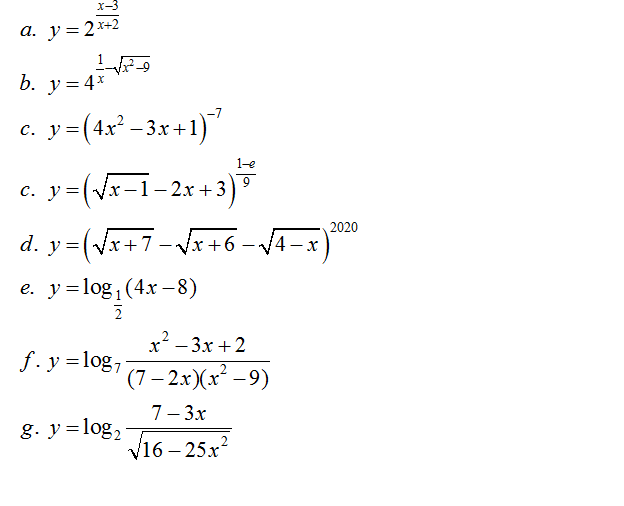
-
TÍNH ĐẠO HÀM CỦA HÀM SỐ
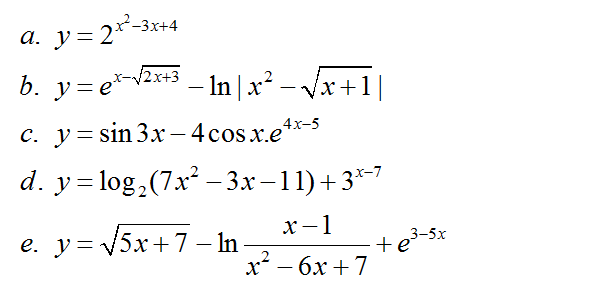
- Hy vọng qua bài dạy sẽ giúp các em có thể ôn tập tốt. Các em có thắc mắc gì hay muốn đi sâu vào thì hãy để lại comment ở Fanpage – You tube hay Website của trường. Cô sẽ giải đáp mọi thắc mắc của các em. Chúc các em học tốt và đạt được nhiều kết cả cao trong kỳ thi sắp tới nhé!
- Học sinh bấm đăng ký kênh youtube của Trường để theo dõi những bài giảng khác nhé!
- Thông tin đăng ký nhập học trường Ngọc Viễn Đông
“NGỌC VIỄN ĐÔNG - MỖI HỌC SINH MỘT VIÊN NGỌC”